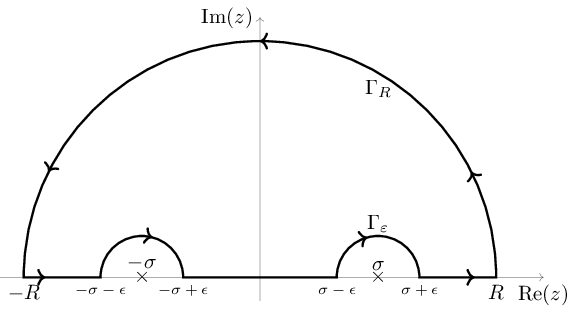
Complex integration path diagram.

This diagram was made for my homework of Mathematical Physics at Drexel University during my Masters education The homework assignment can be found here at http://physics.drexel.edu/~pgautam/courses/

\begin{tikzpicture}
  [
    decoration={
      markings,
      mark=at position  0.10 with {\arrow[line width=1pt]{>}},
      mark=at position  0.20 with {\arrow[line width=1pt]{>}},
      mark=at position  0.30 with {\arrow[line width=1pt]{>}},
      mark=at position  0.50 with {\arrow[line width=1pt]{>}},
      mark=at position  0.70 with {\arrow[line width=1pt]{>}},
      mark=at position  0.80 with {\arrow[line width=1pt]{>}},
      mark=at position  0.90 with {\arrow[line width=1pt]{>}},
    },
    axes/.style={line width=0.1pt,->,opacity=.6, text opacity=1},
    small/.style={font=\scriptsize}
  ]
  \tikzmath{\R=4;\r=0.7;}% Change these values to see the magic
  \draw [axes] (-\R*1.1,0) -- (\R*1.2,0) coordinate (xaxis) node [below] {Re$(z)$};
  \draw [axes] (0,-0.1*\R) -- (0,\R*1.1) coordinate (yaxis) node [left] {Im$(z)$};
  \node at (-0.5*\R,0) {$\times$};
  \node at(-0.5*\R,0) [above] {$-\sigma$};
  \node at (0.5*\R,0) {$\times$};
  \node at (0.5*\R,0) [above] {$\sigma$};

  \path [draw, line width=1.0pt, postaction=decorate]
      (0,0)
      -- (0.5*\R-\r,0) node [below,small]{$\sigma-\epsilon$}
      arc (180:0:\r)   node [below,small]{$\sigma+\epsilon$}
      --  (\R,0) node [below] {$R$}
      arc (0:180:\R) node [below] {$-R$}
      -- (-0.5*\R-\r,0) node [below,small] {$-\sigma-\epsilon$}
      arc (180:0:\r) node [below,small] {$-\sigma + \epsilon$}-- cycle;

  \node at (0.5*\R,1.3*\r) {$\Gamma_{\varepsilon}$};
  \node at (0.5*\R,0.8*\R) {$\Gamma_{R}$};
\end{tikzpicture}