MNIST Handwriting Recognition with Neural Network

In the previous post we discussed how to make functional Neural Network (NN) with julia. In another post we discussed how to package our NN into an independent julia package. As described in that post, we are able to import the new package as

using PNN

Here PNN is the new NN package that we have written from scratch.

One of the most common test cases for new Machine Learning algorithms is, the publicly availabel MNIST human handwriting dataset. We can use that dataset to train and test our new Neural network to verify that this package can indeed be used in real world application. It kind of blows my mind that such a simple little manipulation of few matrices can do such a complex task as handwriting recognition, but anyway here we are.

You can read more about the MNIST Dataset, here. In julia we can use Datasets package to basically get the dataset.

Bit on the Handwriting Recognition Problem

A bit on the handwriting recognition problem Handwriting Recognition Problem. Imagine a set of different picture with handwriting from different people. If we are to write a declarative procedure to do handwriting recognition, we would have to write code to go through each pixel of the picture and come up with some logic that is consistant with the variations the shapes and all the other quircks that come with the handwriting of different people. This becomes an incredibly difficult problem to gather knowledge of the variations in handwriting of different people. And then to come up with and idea to consistantly have a correct comparison is even greater problem.

MNIST Dataset

MNIST handwriting dataset is a collection of handwriting from different people. The images consist of handwritten digits from 0-9 from different people. The idea is to identify what digit does the shape in the given picture correspond to. The MNIST handwriting dataset is freely available to download. You can read more about this here.

In julia we can import the MNIST handwriting dataset by using the MLDatasets package.

using MLDatasets: MNIST

This dataset is divided into two parts, the test datasets and the train datasets. We can access the train dataset with

dataset = MNIST(:train)

dataset MNIST:
  metadata  =>    Dict{String, Any} with 3 entries
  split     =>    :train
  features  =>    28×28×60000 Array{Float32, 3}
  targets   =>    60000-element Vector{Int64}

As we can see there are 60,0000 images with each image being a 28x28 pixel of grayscale values from 0 to 1 0 representing transparent and 1 representing completely opaque. So the actual dataset in essense is a 3D array of dimension \(28 \times 28 \times 60000 \). Here is an example of one such image:

Setup of problem

The train dataset also has the corresponding digit assiciated with it. So each of the 60,000 images have a number corresponding the digit that is written in the image. We can use this 3D arary of 28x28x60,000 along with the knowledge what digit each image correspond to, to train a supervised learnign algorithm to later test an unknown digit.

We can be a bit clever here, so instead of using 60,000 individual number we will use 60,000x10 arary to corcorrespond the position of the digit. This 10 bit string of digits would be have a value close to 1 for the position that the digit in the image represents. For example 0010000000 would correspond to digit 2 and 0001000000 would correspond to digit 3 and so on. So that we design a network that has 28x28 input nods and 10 output nodes. For each image, the value in the corresponding position in the, 10 bit string, would be the probability that the give image is that digit.

So we can use a little module to transform the dataset from the actual MNIST dataset to our purposes.

function prepare(ds)
    X::Vector{Vector{Float64}} = map(x->vec(ds.features[:,:,x]),1:length(ds))
    y = map(x->map(p -> x==p ? 1 : 0,0:9),ds.targets)
    return X,y
end

Building a Network.

Building a network is as easy as setting up a NN object with appropriate number of input and output nodes. For our purposes the number of input nodes is the total number of floating point number representing the image which is \(28 \times 28\). And the number of output nodes is \(10\).

We have a choice of how many hidden layers we want. We can experiment with the number of hidden layers but at the moment lets just start with 1 hidden layer with 30 nodes. So our hidden layer object would be hl = [30]

This setup is very easy with just

tnn = NN(28*28,100,hl=[30])

All the setup is now done. The next step is to just feed in the training dataset to the network.

Training the ntwork

Training the ntework is again as easy as just feeding the trainign dataset. Lets get the transformed dataset first.

X,y = prepare(dataset)

Here dataset object is the previously obtained MNIST dataset.

The other choice of free parameter in our network is the learnign rate and the number of epochs we want to train to. Lets for a start choose learning rate β=0.001; and the number of epochs to 20.

errors = fit!(tnn,X,y;β=0.001,epoch=20)

The errors object returned here contains the error in each epochs. Lets look at error at the end of each epoch for our 20 epochs.

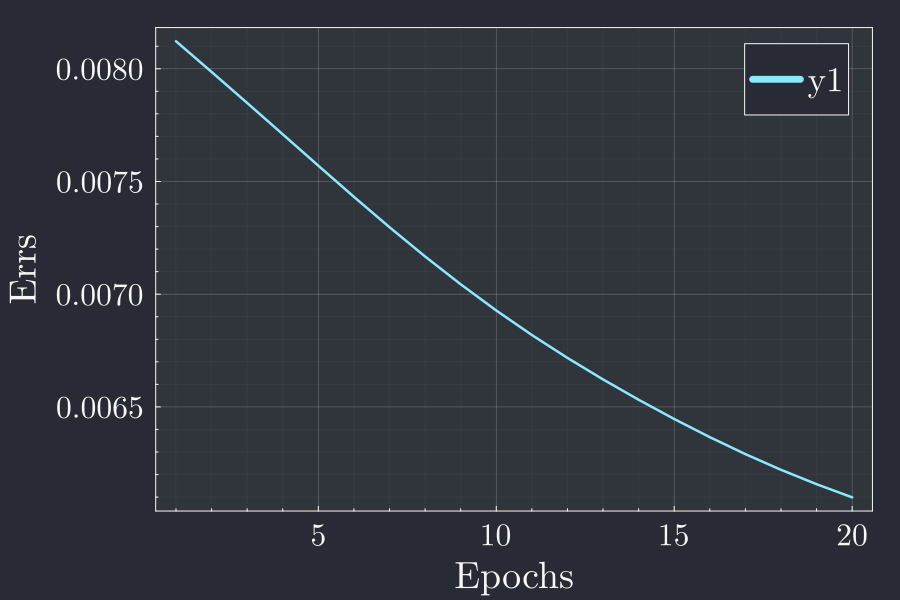
As we can see, at the end of each epoch the error is going down. If you remember from previous post you will know that the error is defined as the sum of squared difference of true value to the value obtained from the network. This y axis in this plot doesn't mean anything by itself, but qualitatively we can say that the error is decreasing each epoch, meaning we are doing better and better after each pass through the network.

Testing the network

How do we know, that the network we just trained is any good. For that purpose the MNIST dataset also has testing dataset which we can obtain simply by using

testds = MNIST(:test)

ataset MNIST:
  metadata  =>    Dict{String, Any} with 3 entries
  split     =>    :test
  features  =>    28×28×10000 Array{Float32, 3}
  targets   =>    10000-element Vector{Int64}

So the test dataset is again 10,000 image of the same size as the train image, which is 28x28 pixels. This dataset also comes with the true value but we wont use it to pass through the network. We will only use this to compare with what comes out of the ntework. We can then count how much we predicted correctly.

Here I have written a simple function which will take the test dataset and pass through the network and store into two arrays for whether each is predicted correctly or incorrectly.

function accuracy(tnn::NN,Xp,yp)
    cor = []
    wrong = []
    for (i,(xt,yt)) = enumerate(zip(Xp,yp))
        ypr = feed!(tnn,xt)
        pd = (findall(x->x==maximum(ypr),ypr) .- 1)[1]
        tr = (findall(x->x==1,yt).- 1)[1]
        if pd == tr push!(cor,(i,xt,pd,tr))
        else push!(wrong,(i,xt,pd,tr)) end
    end
    return cor,wrong
end

As we did before we can again prepare the test dataset, calculate the accuracy. The transformed test dataset are now

Xs,ys = prepare(testds)

We can now pass this and print how much we got correct.

cor,wrong = accuracy(tnn,Xs,ys);
cl,wl = length(cor),length(wrong)
print("# $epoch epoch $(hl) hl : $cl correct out of 10000 and $wl wrong. Accuracy $(cl/100)% β=$β")

# 20 epoch [30] hl : 9285 correct out of 10000 and 715 wrong. Accuracy 92.85% β=0.001

Similarly with other runs of differen parameters we got:

# 30 epoch 60 hl     : 9718 correct out ot 10000 and 282 wrong. Accuracy 97.18% β=0.1
# 50 epoch 60 hl     : 9745 correct out ot 10000 and 255 wrong. Accuracy 97.45% β=0.09
# 10 epoch [60] hl   : 9701 correct out of 10000 and 299 wrong. Accuracy 97.01% β=0.08
# 6 epoch [100] hl   : 9678 correct out of 10000 and 322 wrong. Accuracy 96.78% β=0.07

As indeed we see that we reach an accuracy of as high as 97.85 which is very accurate considering we only wrote like handful of lines of code.

I have a handy little function that also shows the visual of each image:

function visual(arry,n)
    i,xt,pd,tr = arry[n]
    heatmap(reshape(xt,28,28)',yflip=true,title="$i. True $tr Predicted $pd")
end

vl = 48
visual(cor,vl)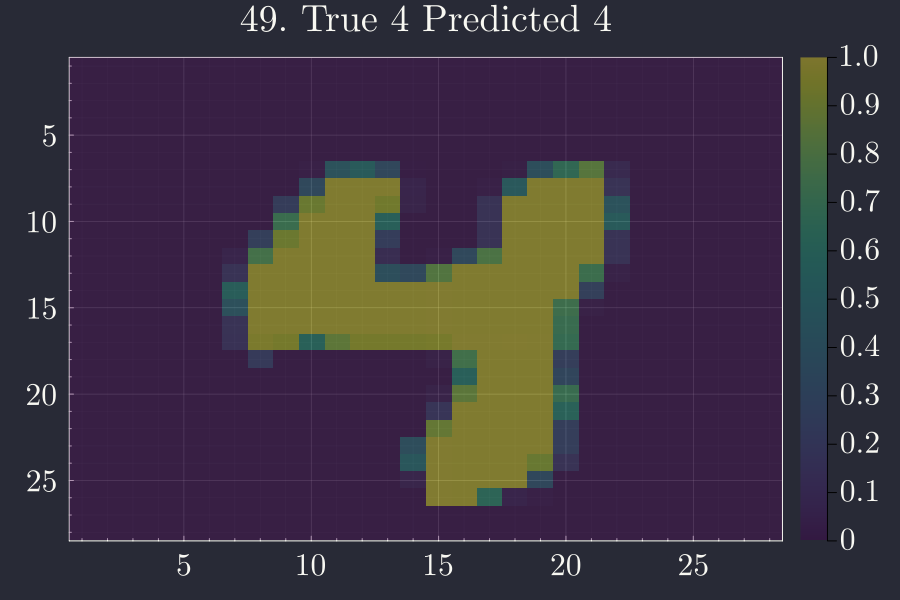

This is indeed beautiful that it works with such a simple function.

N.B.: I have completely lost interest in writing properly about ML and stuffs. This is too much of basic stuff to dwell on. I am trying to get rid of this bad habit of working on trivial problem and move on to work on problems that matter, which obviously is playing tennis in the weekend.