Dice Wars game
Dicewars
A simplified version of game DiceWars between two players goes such that each player is assigned a stack of 6-sided dice which equate to relative power. On a player's turn, the player challenges other player. The challenge is resolved when each player rolls their dice, with the higher total winning.
Each player roll all of their dices and the value at the top of each dice is added to find the players score. Whoever has the higher score wins and the equal score is a tie. The goal is to find the probability that, in a game between two players with \(m\) and \(k\) dice respectively, any player wins over the other or there is a tie.
Before we calculate the probability of win or a draw, lets calculate the probability that a player with \(k\) dices rolls a total of \(n\). Since for a standard dice the number on each face is one of \({1,2,3,4,5,6}\). When the player rolls \(k\) dices the minimum sum is \(k\) when each dice rolls to be \(1\) and a maximum of \(6k\) when each one rolls to be \(6\) thus \(k \leq n \leq 6k\).
The total exhaustive cases of rolling \(k\) dice is \(6^k\). The total possible ways we can get a sum of \(n\) (subject to above constraint) when we roll \(k\) dice is the same as the total number of ways we can write \(n\) as a sum of \(k\) integers such that each integer\(n_i\) is between \(1 \leq n_i \leq 6\). The order of integers that we break the number \(n\) is important too.
Lets us define a function \(f_k(n)\) such that it gives the total number of ways we can break \(n\) into \(k\) integers where each integer is one of \({1,2,3,4,5,6}\)
Because of the constraint \(k \leq n \leq 6k\) we can immediately write
It is not hard to see the constraint
These are the edge cases we can identify because of constraints in hand. Before trying to find the function for general \(k\) and \(n\) lets try a special case.
For a special case of \(f_3(7)\), i.e., the number of ways we can express \(7\) as a sum of \(3\) integers between \(1\) and \(6\)
We can write \(7\) as a sum of \(2\) integers as \(1 + 6\) or \(2 + 5\) or \(3 + 4\) or \(4 + 3\) or \(5 + 2\) or \(6 + 1\). There are a total of \(6\) ways we can do it. But if we want to express it as sum of \(3\) integers then we can write the second integer as a sum of \(2\) integer. Then the number of ways we can express \(7\) as a sum of three integers becomes the sum of the number of ways we can express 6 as sum of 2 integers plus the number of ways we can write 5 as a sum of 2 integers and so on.
This leads us to write
This suggests us a general expression for \(k \geq 2\)
This is a recursive function the general expression for all \(k\) then is
Below is a python function that calculates this function
def F(k,n,minno=1,maxno=6):
if n < 1 or n < k:
return 0
if k == 1:
return 0 if n > maxno else 1
else:
return sum([F(k-1,n-i) for i in np.arange(minno,maxno+1,1)])The probability \(p_k(m)\) that we get a total of \(n\) when we roll \(k\) dice can then simply becomes
Where the denominator is the number of all possible ways of rolling \(k\) dice.
Below is a python function that calculates this probability
def p(k,n,dice_op=np.arange(1,6+1,1)):
return F(k,n)/len(dice_op)** k #len (dice_op) is just 6Before we go to the game of win an draw lets see graphically how do the number look like. The plot below shows the count (left) and probability(right) of the sum (x-axis) when \(m\) dice (inset) are rolled
def plot_counts(ms,dice_op=np.arange(1,6+1,1),plpr=False,ax=None):
for m in ms:
total_op = len(dice_op)**int(m)
ns = np.arange(m,6*m+1,1)
cnts = [F(m,n) for n in ns]
pvl = np.array(cnts)/total_op if plpr else cnts
ax.plot(pvl,'-o',label=f'm={m}')
ax.legend()fig,ax = plt.subplots(1,2,figsize=(18,6),sharex=True)
plot_counts([1,2,3,4],plpr=False,ax=ax[0])
plot_counts([1,2,3,4],plpr=True,ax=ax[1])
ax[0].set_xlabel('Sum'); ax[0].set_ylabel('Count')
ax[1].set_xlabel('Sum'); ax[1].set_ylabel('pmf');
plt.tight_layout()
plt.savefig('Prob_count',dpi=120,bbox_inches='tight')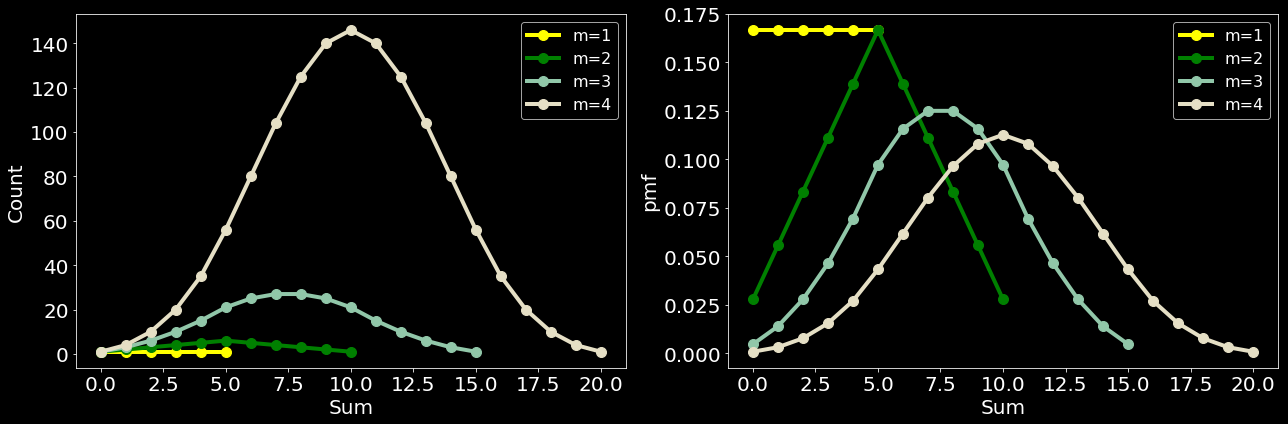
Probability of tie
The pobability of tie in a game of two players throwing \(k\) and \(m\) die respectively is simply the probability that they roll the same sum. The set of possible sum of player with k die is
Similarly for other player
Which can be easily written as
The python function for this written as
def get_tie_prob(m,k):
n1 = np.arange(m,6*m+1,1)
n2 = np.arange(k,6*k+1,1)
return sum([p(m,n)*p(k,n) for n in n1 if n in n2])I have this helper function that calculates generates the table of values.
def generate_table(ms,ks,func=get_tie_prob):
prob_table = np.zeros(shape=(len(ms),len(ks)))
for m in ms:
for k in ks:
prob_table[m-1][k-1] = func(m,k)
df = pd.DataFrame(prob_table,columns=ms,index=ks)
return dfLets say \(ms\) is the set of number of dice player1 has and \(ks\) be the number of dice playe 2 has then
maxn=6
ms = ks = np.arange(1,maxn+1,1)%time tie_prob_table = generate_table(ms,ks,get_tie_prob)CPU times: user 2.29 s, sys: 18.3 ms, total: 2.31 s Wall time: 2.29 s
tie_prob_table| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 0.166667 | 0.069444 | 0.015432 | 0.001929 | 0.000129 | 0.000004 |
| 2 | 0.069444 | 0.112654 | 0.069444 | 0.024884 | 0.005955 | 0.001017 |
| 3 | 0.015432 | 0.069444 | 0.092850 | 0.065469 | 0.029940 | 0.009822 |
| 4 | 0.001929 | 0.024884 | 0.065469 | 0.080944 | 0.061479 | 0.032624 |
| 5 | 0.000129 | 0.005955 | 0.029940 | 0.061479 | 0.072693 | 0.057935 |
| 6 | 0.000004 | 0.001017 | 0.009822 | 0.032624 | 0.057935 | 0.066539 |
The probability of tie when players have \((m,k)\) dice respectively corresponds to the cell \((m,k)\) in the table above.
The probability for win
Similarly the probability of win for player with \(m\) dice is the probability that the player \(k\) throws a sum \(i\) times the sum of probabilities of ways player \(m\) throws \(j\) dice such \(j > i\)
The python function implementing this function is
def get_win_prob(m,k):
if m > k:
wkm = get_win_prob(k,m)
tkm = get_tie_prob(k,m)
return 1 - wkm - tkm
n1s = np.arange(m,6*m+1,1)
n2s = np.arange(k,6*k+1,1)
win_prob = sum([p(k,i) * sum([p(m,j) for j in n1s if j > i]) for i in n2s])
return win_probGenerating the table
win_prob_table = generate_table(ms,ks,get_win_prob)
display(win_prob_table)| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 0.416667 | 0.092593 | 0.011574 | 0.000772 | 0.000021 | 0.000000 |
| 2 | 0.837963 | 0.443673 | 0.152006 | 0.035880 | 0.006105 | 0.000766 |
| 3 | 0.972994 | 0.778549 | 0.453575 | 0.191701 | 0.060713 | 0.014879 |
| 4 | 0.997299 | 0.939236 | 0.742831 | 0.459528 | 0.220442 | 0.083423 |
| 5 | 0.999850 | 0.987940 | 0.909347 | 0.718078 | 0.463654 | 0.242449 |
| 6 | 0.999996 | 0.998217 | 0.975300 | 0.883953 | 0.699616 | 0.466731 |
The probability of win for player \(m\) when players have \((m,k)\) dice respectively corresponds to the cell \((m,k)\) in the table above.