We are going to calculate the average kinetic energy of particles whose velocity follow Maxwell’s distribution.
We know that the Maxwell’s velocity distribution function is given by the following relation.
\[
\begin{aligned}f(v) = Av^2e^{-mv^2/2kT}\end{aligned}
\]
Here, \(A\) is a normalization constant, \(m\) is the mass of each particle, \(k\) is Boltzmann’s constant, and \(T\) is the temperature of the system.
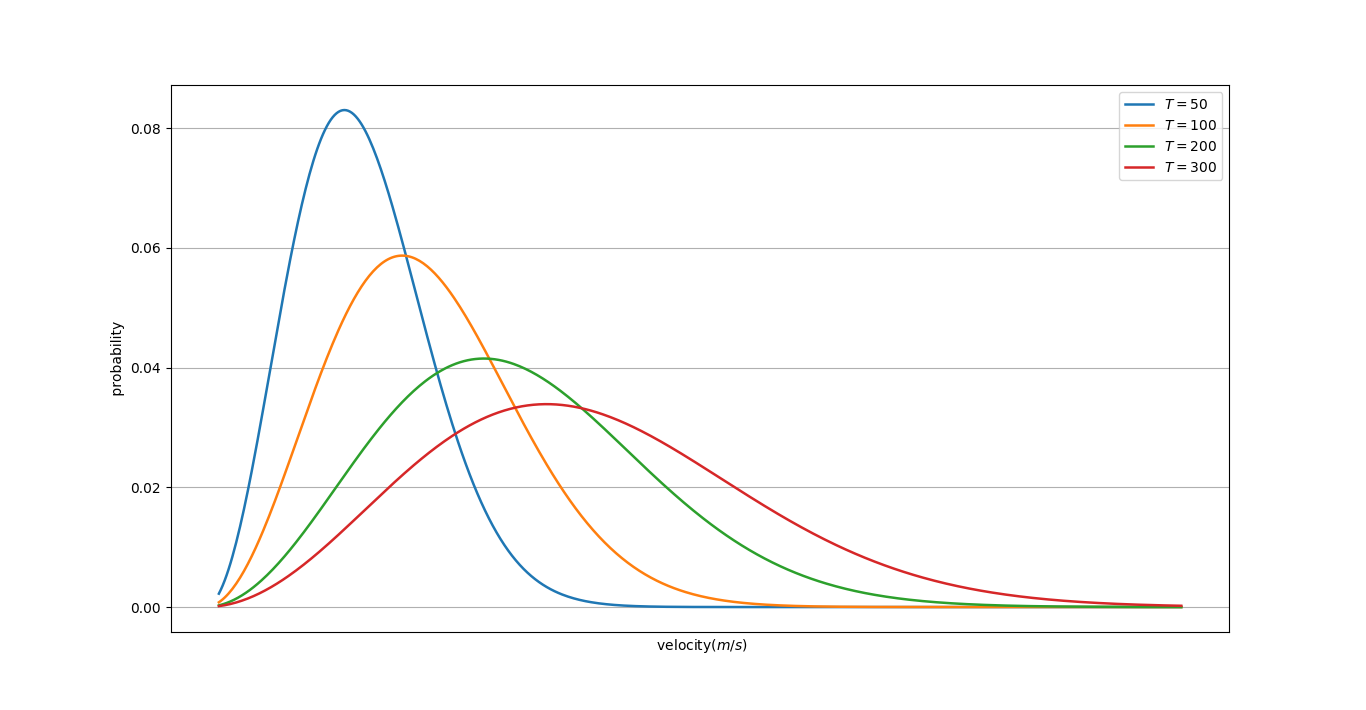
The plot of this distribution looks like
The normalization condition gives
\[
\begin{aligned}\int\limits_0^\infty
f(v)dv = \int\limits_0^\infty
Av^2e^{-mv^2/2kT}dv = 1\end{aligned}
\]
To carry out the integration lets make some change of variables
\[
\begin{aligned}\frac{mv^2}{2kT} = x; \qquad \Rightarrow
v = \sqrt{\frac{2kT}{m}x};\quad dv = \frac{kT}{mv}dx, \qquad \text{As }v \rightarrow
\{0,\infty\}\quad x \rightarrow
\{0,\infty \}\end{aligned}
\]
Using these variable transformation, our normalization integral becomes.
\[
\begin{aligned}A \int\limits_0^\infty
v^2e^{-x} \frac{kT}{mv} dx &= A \int\limits_0^\infty
\frac{kT}{m} \sqrt{\frac{2kT}{m}x}e^{-x}dx\\
& = A \sqrt{2}\left( \frac{kT}{m}\right)^{\frac{3}{2}}\int\limits_0^\infty
\sqrt{x}e^{-x}dx = 1\end{aligned}
\]
But by definition of gamma function \(\Gamma(n) =\int\limits_0^\infty
x^{n-1}e^{-x}\) we get. And \(\Gamma\left(\frac{3}{2}\right) = \frac{1}{2} \Gamma \left( \frac{1}{2}\right)
{1}{2} = \frac{1}{2}\sqrt{\pi}\)
\[
\begin{aligned}A \sqrt{2}\left( \frac{kT}{m}\right)^{\frac{3}{2}}\int\limits_0^\infty
x^{\frac{3}{2}-1}e^{-x}dx &= A\sqrt{2} \left( \frac{kT}{m}\right)^{\frac{3}{2}} \Gamma\left(\frac{3}{2}\right) =1 \qquad \\
\Rightarrow A &= \frac{1}{\frac{1}{2}\sqrt{2\pi}\left( \frac{kT}{m} \right)^{\frac{3}{2}}}\end{aligned}
\]
The expectation value for the square of speed can be calculated as:
\[
\begin{aligned}\langle v^2 \rangle = \int\limits_0^\infty
v^2 f(v)dv = A \int\limits_0^\infty
v^4 e^{-mv^2/2kT}
dv\end{aligned}
\]
Carrying out same transformations as above we get.
\[
\begin{aligned}\langle v^2 \rangle &= A \int\limits_0^\infty
2^{\frac{3}{2}}\left(\frac{kT}{m}\right)
^{\frac{5}{2}}x^{\frac{3}{2}}e^{-x}dx\\
& = A 2^{\frac{3}{2}}\left(\frac{kT}{m}\right)
^{\frac{5}{2}} \int\limits_0^\infty
x^{\frac{5}{2}-1}e^{-x}\\
&= A 2^{\frac{3}{2}}\left(\frac{kT}{m}\right)
^{\frac{5}{2}} \Gamma \left( \frac{5}{2}\right)\\
&= A 2^{\frac{3}{2}}\left(\frac{kT}{m}\right)
^{\frac{5}{2}} \frac{3}{4}\sqrt{\pi} \\
& = \frac{1}{\frac{3}{2}\sqrt{2\pi}\left( \frac{kT}{m} \right)^{\frac{3}{2}}} \times 2^{\frac{3}{2}}\left(\frac{kT}{m}\right)
^{\frac{5}{2}} \frac{3}{4}\sqrt{\pi}\\
& = \frac{3kT}{m}\\
\Rightarrow \frac{1}{2}m\langle v^2 \rangle &= \frac{3}{2}kT\end{aligned}
\]
So the average kinetic energy of particles at temperature \(T\) whose velocity distribution is Maxwell’s distribution is \(KE = \frac{3}{2}kT\)
