In most simplified scenarios we ignore the role of air drag on the body under the influence of gravitataion. A good approximation for the air drag force is that it is proportional to the speed of the body.
Lets suppose a body of mass \(m\) is thrown upward with initial speed \(v_0\) .The drag force from the air is \(\vec{F}=-\alpha m \vec{v}\). Choosing coordinate axis to be such that the upward direction is positive \(Z\) axis.
\[
\begin{aligned}\vec{v}=v\vec{\hat{z}}\end{aligned}
\]
The total force acting on the ball is thus:
\[
\begin{aligned}\vec{F}_t=-\alpha m v\vec{\hat{z}}-mg \vec{\hat{z}}\end{aligned}
\]
By using Newton’s second law of motion we get;
\[
\begin{aligned}m\dot{v}\vec{\hat{z}} &= -\alpha m v\vec{\hat{z}}-mg \vec{\hat{z}}\end{aligned}
\]
\[
\begin{aligned}\dot{v} + \alpha v – g &= 0\end{aligned}
\]
Eq. ((1)) can be solved with the use of integrating factor. \(I = e^{\alpha t}\). Thus
\[
\begin{aligned}e^{\alpha t}\dot{v} + \alpha e^{\alpha t} v + ge^{\alpha t} = 0\end{aligned}
\]
\[
\begin{aligned}\frac{d}{dt}\left(e^{\alpha t}v \right) + ge^{\alpha t} = 0\end{aligned}
\]
Thus,
\[
\begin{aligned}e^{\alpha t}v = -g \int e^{\alpha t} dt\end{aligned}
\]
\[
\begin{aligned}e^{\alpha t}v = -\frac{g}{\alpha} e^{\alpha t} + k\end{aligned}
\]
We have at \(t = 0\) the speed \(v(0) = v_0\). Which gives \(k = v_0 + v_t\); where \(v_t = \frac{g}{\alpha}\)
\[
\begin{aligned}e^{\alpha t} v(t) = (v_0 + v_t) – v_t e^{\alpha t}\end{aligned}
\]
Thus,
\[
\begin{aligned}v(t) = -v_t + (v_0 + v_t) e^{-\alpha t}\end{aligned}
\]
Eq. ((2)) gives us the speed of the body as a function of time. If there was no air drag; i.e., \(\alpha = 0\) it correctly reduces down two \(v(t) = v_0 – gt\). It can be solved to get the position of the body as a function of time. We have.
\[
\begin{aligned}z(t) &= \int_0^t v(t)dt = \int_0^t -v_t + (v_0 + v_t)e^{-\alpha t}dt \\
{} &= \left[ -v_tt -\left(\frac{v_0 + v_t}{\alpha}\right)e^{-\alpha t} \right]_0^t \\
{} &= \left[ -v_tt -\left(\frac{v_0 + v_t}{\alpha}\right)e^{-\alpha t} + \left(\frac{v_0 + v_t}{\alpha}\right)\right]\end{aligned}
\]
\[
\begin{aligned}z(t) &= -v_tt + \frac{1}{\alpha}(v_0 + v_t)\left( 1 – e^{-\alpha t} \right)\end{aligned}
\]
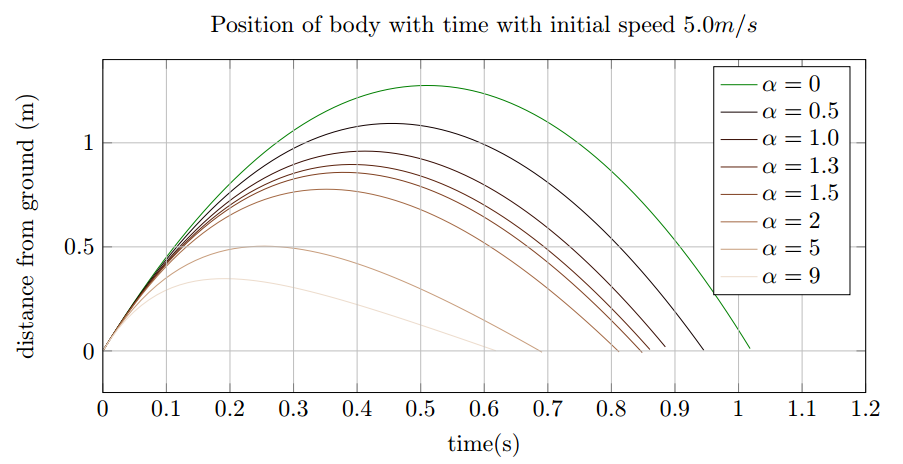
As shown in Fig. (1) we see that the commonly used quardratic approximation in the absence of air resistance is the limiting case of \(z(t)\) as \(\alpha \rightarrow 0\). And with increase int the drag constant \(\alpha\) the body attains terminal velocity as evinced by the unsymmetrical nature of the graph in the descent with the segment nearly linear.
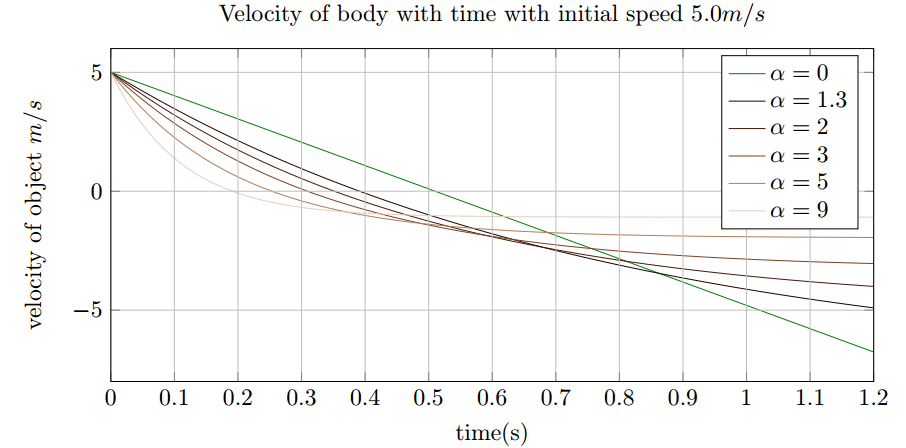Fig. (2) shows the velocity of the body with time.
When the drag constant is zero, i.e., we ignore air resistance.
velocity \(v(t)\) as \(\alpha = 0\)
We have
\[
\begin{aligned}e^{-\alpha t} = 1 – \alpha t + \frac{\alpha^2t^2}{2!} + …\end{aligned}
\]
From Eq. ((2)) we have
\[
\begin{aligned}v(t) = -\frac{g}{\alpha} + \left(v_0 + \frac{g}{\alpha}\right)(1-\alpha *t + O(\alpha^2))\end{aligned}
\]
\[
\begin{aligned}\lim_{\alpha \rightarrow 0} v(t) &= \lim_{\alpha \rightarrow 0} \left( -\frac{g}{\alpha} + v_0 – gt + \frac{g}{\alpha} – v_0\alpha t + O(\alpha^2)\right) \\
v(t) &= v_0 – gt\end{aligned}
\]
distance \(z(t)\) as \(\alpha = 0\)
From Eq. ((3)) we have
\[
\begin{aligned}z(t) &= -\frac{g}{\alpha}t + \frac{1}{\alpha}\left(v_0 + \frac{g}{\alpha} \right)\left( 1 -\left\lbrace 1 – \alpha t + \frac{\alpha^2t^2}{2}+ …\right\rbrace \right) \\
{} &= -\frac{g}{\alpha}t +\left( \frac{v_0}{\alpha} + \frac{g}{\alpha^2} \right)\left(\alpha t – \frac{\alpha^2t^2}{2}+ O(\alpha^3)\right) \\
{} &= v_0t – \frac{1}{2}gt^2 + f(\alpha)\end{aligned}
\]
Thus
\[
\begin{aligned}\lim_{\alpha \rightarrow 0} z(t) &= \lim_{\alpha \rightarrow 0} v_0t – \frac{1}{2}gt^2 + f(\alpha) \\
z(t) &= v_0t – \frac{1}{2}gt^2\end{aligned}
\]
For the case where the air air drag is zero, we get our familiar kinematic euqation as expected.